Abstract

이전 포스트에서 기관, 외인순매매량과 주가의 관계를 삼성전자, 대한항공 2가지의 예시로 간략하게 살펴보았으며 뚜렷한 결과를 확인하기는 힘들었다. 그래서 이번에는 2020년 12월 31일 기준 코스피에 상장된 총 799개의 종목을 이용해 주가와의 관계를 살펴보고자 한다. 여기서 순매매량은 기관, 외인의 순매매량과 당일 종가를 곱한 값을 사용했다(액면분할등의 이슈로 주가가 급변할 경우 거래량도 급변하기 때문).
기관 외국인 거래량(x)와 주가(y)의 관계를 시계열 회귀, LSTM 등의 예측기반 방법론을 통해 살펴볼수도 있지만, 아직까지 시계열 데이터를 예측하는 방법론들에 익숙하지 않고, 또 두 변수의 긴밀한 관계도 없을 것이라고 생각되므로 위의 방법론을 이용한 예측은 추후에 기회가 된다면 다뤄보기로하고, 이번 포스트에서는 기관, 외인 거래량이 급증(or 급락)했을 때 해당 주가의 변동에 초점을 맞추어 살펴보기로 했다. 그리고 결과는 예상했던것과 다르게 기관, 외인 거래량이 급증, 급락한 두가지 경우 모두 주가에 좋지않은 영향을 가져다 주었다.

세부 전략

그렇다면 위에서 말한 기관, 외인 거래량이 급변했다는 것을 어떻게 알 수 있을까?
보통 이상감지(Anormaly Detection) 와같은 방법을 사용하며 여기서는 Z-score normalization(정규화)를 통해 특정값(여기서는 2.5)이상인 값을 이상치로 분류했다.
처음에는 단순히 기관과 외인의 순매매량을 정규화해 값이 크거나 작은 지점들을 선택했다.

# import library ~ Preprocessor 객체생성까지는 이전포스트 참조

class TradeStradegy:
    '''
    mergePrice: 기관, 외인 데이터베이스로부터 추출된 데이터프레임과
    주가 데이터베이스로부터 추출된 데이터프레임 결합
    
    stradegy1Condition: 기관, 외인 순매매량의 이상치 index 반환
    
    stradegy1: 위의 index를 기준으로 n일 후 종가 변화량들 반환
    '''
    def __init__(self, code, criteria, window, dayLater, who):
        self.code = code
        self.criteria = criteria
        self.window = window
        self.dayLater = dayLater
        self.who = who
        self.curC = conStock.cursor()
        self.curP = conPrice.cursor()
        self.df = self.mergePrice()
        
    def mergePrice(self):
        dfWho = extractDf(self.curC, self.code)
        dfPrice = extractDf(self.curP, self.code)
        
        dfWho['Date'] = pd.to_datetime(dfWho['Date'])
        dfWho['volumePrice'] = dfWho[self.who]*dfWho['Close']
        dfWho = dfWho.drop(columns = ['Close','Change','Volume'])
        df = dfWho.merge(dfPrice,how='left',on='Date')
        df = df[::-1].reset_index(drop=True)
        return(df)
    
    
    def stradegy1Condition(self):
        ppsr = Preprocessor
        self.df['volumePriceRolling'] = ppsr.normalize(self.df['volumePrice'].rolling(window=self.window).mean())
        if(self.criteria>0):
            plusIdx = self.df[self.df['volumePriceRolling']>self.criteria].index.values
        else:
            plusIdx = self.df[self.df['volumePriceRolling']<self.criteria].index.values
        
        if(len(plusIdx)==0):
            return np.array([])
        uniqueIdx = [plusIdx[0]]
        for i in range(1,len(plusIdx)):
            if(plusIdx[i] - plusIdx[i-1] > 5):
                uniqueIdx.append(plusIdx[i])
        return np.array(uniqueIdx)
    
    def stradegy1(self): #or inst_sum
        uniqueIdx = self.stradegy1Condition()
        uniqueIdxLater = uniqueIdx + self.dayLater

        uniqueIdx = uniqueIdx[uniqueIdxLater<len(self.df)]
        uniqueIdxLater = uniqueIdxLater[uniqueIdxLater<len(self.df)]
        
        
        dfOrigin = self.df.iloc[uniqueIdx,:]
        dfLater = self.df.iloc[uniqueIdxLater,:]
        return (dfLater['Close'].values/dfOrigin['Close'].values,
                np.random.choice(self.df[self.dayLater:]['Close'].values / self.df[:-1*self.dayLater]['Close'].values, len(uniqueIdx)))
#        return (1-np.mean(dfSelected['Close']/dfSelected['Open']), len(dfSelected))

tss = TradeStradegy('c005930', 2.5, 10, 30, "inst_sum")
df = tss.mergePrice()

fig = df.iplot(x='Date', y='volumePrice', asFigure=True, title='삼성전자 기관 순매매량')
fig.show()

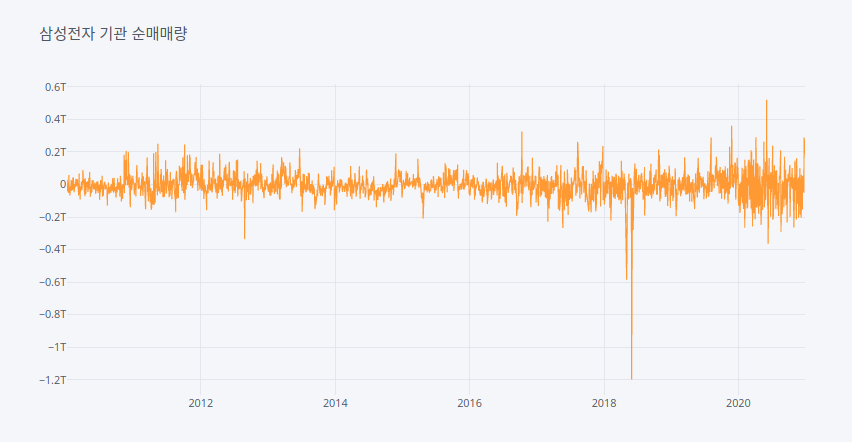하지만 위의 그래프에서 보는 바와같이 일일 순매매량 변동이 너무 크기때문에 10일 이동평균(Moving average)변환을 이용해 변동을 줄인 후 정규화를 진행했고, 이 값이 2.5보다 큰 지점을 파란선으로 표시했다.

ppsr = Preprocessor
df['vPR'] = df['volumePrice'].rolling(window=10).mean()
df['vPRNM'] = ppsr.normalize(df['vPR'])

fig = df['vPRNM'].iplot(asFigure=True, title='삼성전자 기관 순매매량(10일 이동평균 + 정규화)')
for i in plusIdx:
   # fig.add_scatter(x=[i]*100, y=np.linspace(-100000,100000,100), opacity=0.3)
    fig.add_trace(go.Scatter(
    x=[i]*100, y=np.linspace(df['vPRNM'].min(),df['vPRNM'].max(),100),
    opacity=0.3,
    marker_color='rgba(0, 0, 158, .8)'
))
fig.show()

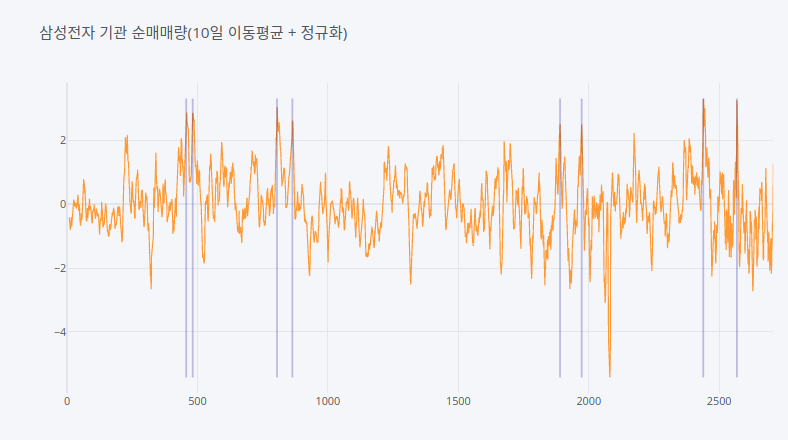10년간 기관 매매량급증은 8회나타났다. 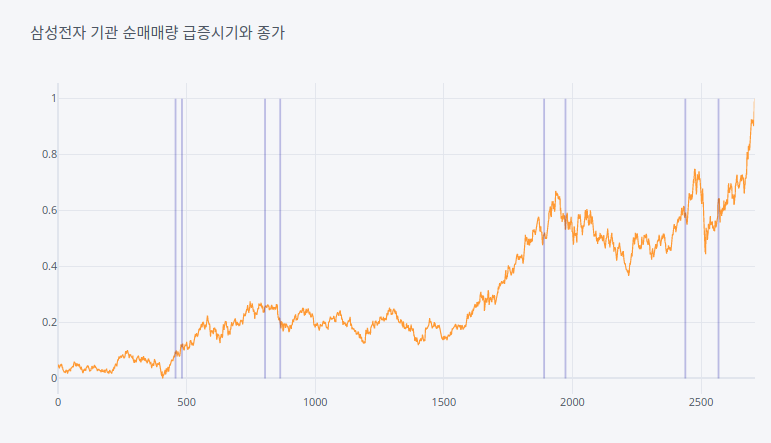위 그래프는 기관 매매량급증신호와 종가를 같이 나타낸 것이다. 삼성전자의 경우 기관매매량이 급증한 경우 대체로 주가가 오르는 경우가 많았다.
이제 삼성전자 단일종목이 아닌 모든 코스피종목에대해 위와같은 기관 매매량급증신호가 나타난 후 30영업일(약 40일)후 주가변화값을 모두 구해보았다.

result = np.array([])
resultRandom = np.array([])
for code in tqdm(codes):
    tss = TradeStradegy(code, 2.5, 10, 30, "inst_sum")
    stdg1 = tss.stradegy1()
    changeSelected = stdg1[0]
    changeRandom = stdg1[1]
    result = np.append(result, changeSelected)
    resultRandom = np.append(resultRandom, changeRandom)
		
print(len(result)
print(np.mean(result))

총 3500번 정도 위와같은 신호에따른 매매를 진행했고, 놀랍게도 평균적으로 1.3%정도 손해를 본다는 결과가 나왔다.

n = 30
allCases = np.array([])
for code in tqdm(codes):
    df = extractDf(conPrice.cursor(), codes[0])
    allCases = np.append(allCases, df[n:]['Close'].values/df[:-n]['Close'].values)
meanList = []
#gmeanList = []

for i in range(1000):
    temp = np.random.choice(allCases, n)
    meanList.append(np.mean(temp))
#    gmeanList.append(gmean(temp))

allCases_ = allCases - 1
result_ = result - 1

n = len(result)
pd.DataFrame({"random": np.random.choice(allCases_, n), "selected": result_}).iplot(kind='histogram', theme='white', title='Strategy1 vs random')

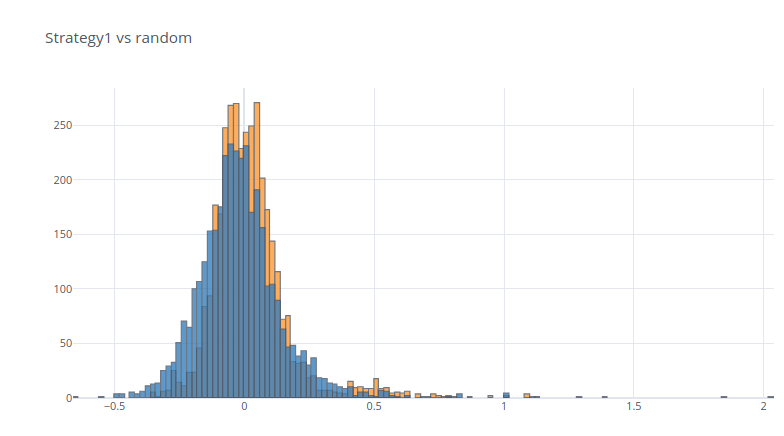Histogram을 통해 확인해보면(x축은 수익률) 신호에 따른 매매가 랜덤한 매매보다 안좋은 결과를 나타냄을 알 수 있다.
마지막으로 bootstrap method를 이용해 위의 결과(평균 1.3% 손해)가 얼마나 통계적으로 유의미한지를 확인해보자.

# bootstrap

meanList = []
for i in range(1000):
    temp = np.random.choice(allCases, n)
    meanList.append(np.mean(temp))
print(np.mean(meanList))
print(min(meanList))

놀랍게도 랜덤한 매매는 30영업일 후 평균 2.1%정도의 수익을 냈고(코스피는 장기적으로 우상향하기때문), 3500개정도를 랜덤하게뽑아 평균을 낸 값중 가장 안좋은 결과도 평균 1.2%의 수익을 내었음을 알 수 있다. 즉 위의 기관 매매량급증 신호에 따른 매매를 할 경우 랜덤한 매매보다도 훨씬 좋지않은 수익률을 기록했음을 알 수 있다.

다음포스트에는 마지막으로 이동평균값, 기관 or 외인, n영업일 후 매매 등과같은 parameter 값들을 달리해 어떤 전략을 취해야 수익을 올릴 수 있는지를 살펴보자.