[Python]k-means 클러스터링 구현
by Edward Park
Abstract
아마 ML algorithm중 가장 이해하기쉽고, 구현도 간단한 알고리즘을 뽑으라면 많은 이들이 k-means clustering을 뽑을것이다. 그래서 한번 구현해보았다.
동작 과정
- hyper-parameter인 k 값을 설정한다.
- k개의 center(중심점)을 무작위로 선택한다. (이때 성능을 좋게하기 위해서 랜덤이 아닌 다른 방법을 사용하기도 함)
- 각각의 x에 대해 가장 가까운 center를 찾고, 이 그룹에 포함시킨다.
- 해당 그룹들의 평균값을 다시 center로 지정한다
- 위의 과정을 k개의 중심점들이 변화가 없을 때 까지 반복한다.
Code
Set data
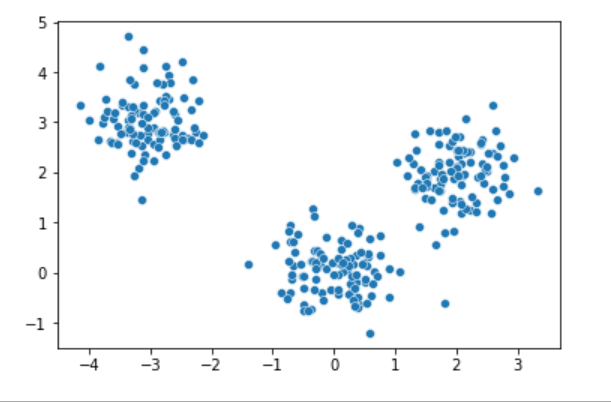
무작위로 x를 뽑는다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
x = [] # data
k = 3 # hyper paramters
np.random.seed(2021)
x.extend(np.random.normal(loc=[0,0], scale=0.5, size=(100, 2)).tolist())
x.extend(np.random.normal(loc=[2,2], scale=0.5, size=(100, 2)).tolist())
x.extend(np.random.normal(loc=[-3,3], scale=0.5, size=(100, 2)).tolist())
x = np.array(x)
sns.scatterplot(x=x[:,0], y=x[:,1]);
 Train Model
Train Model
def distance(a, b):
return sum((a - b) ** 2)/len(a)
def group_center(g):
g = np.array(g)
return g.mean(axis=0)
def cluster(x, k, seed=2022, iter_num=25):
logs = []
np.random.seed(seed)
centers = x[np.random.choice(len(x), size=k, replace=False)]
for it in range(iter_num):
group = {}
for i in range(k):
group[i] = []
# find nearest center
for row in x:
temp = []
for i in range(k):
temp.append(distance(centers[i], row))
group[np.argmin(temp)].append(row.tolist())
# plot data store
for i in range(k):
group_temp = np.array(group[i])
group_temp = np.c_[group_temp, np.full(len(group_temp), i)]
if i == 0:
grouped = group_temp
else:
grouped = np.append(grouped, group_temp, axis = 0)
# update center
centers_new = []
for i in range(k):
centers_new.append(group_center(group[i]).tolist())
centers_new = np.array(centers_new)
# if updated center == center, break
if np.sum(centers - centers_new) == 0:
break
else:
centers = centers_new
logs.append(grouped)
return grouped, logs, it
grouped, logs, it = cluster(x, 3)
print(f'iter num:{it}')
Plotting
plt.figure(figsize=(15,8))
for i in range(it):
plt.subplot(2, it//2+1, i+1) # row, col, index
df = pd.DataFrame(logs[i])
df.columns = ['x1', 'x2', 'group']
sns.scatterplot(data = df, x = 'x1', y = 'x2', hue = 'group').set_title(f'iter : {i}')
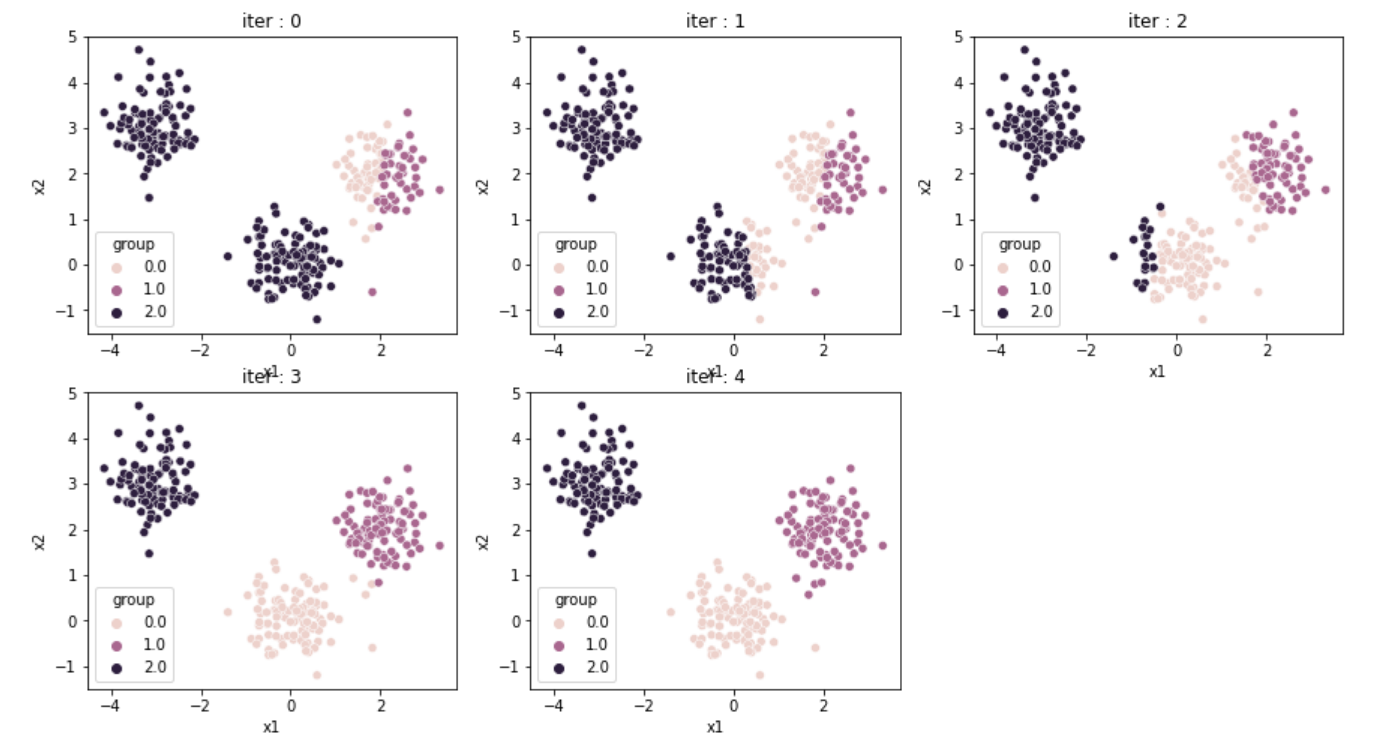 5번의 시행만에 군집을 분리해냈다. 뚜렷히 구분이 되어있는 데이터들에 대해서는 좋은 성능을 보여준다.
5번의 시행만에 군집을 분리해냈다. 뚜렷히 구분이 되어있는 데이터들에 대해서는 좋은 성능을 보여준다.
단점
x = [] # data
k = 3 # hyper paramters
np.random.seed(2021)
x.extend(np.random.normal(loc=[0,0], scale=0.5, size=(100, 2)).tolist())
x.extend(np.random.normal(loc=[1,2], scale=0.5, size=(100, 2)).tolist())
x.extend(np.random.normal(loc=[1,3], scale=0.5, size=(100, 2)).tolist())
x = np.array(x)
sns.scatterplot(x=x[:,0], y=x[:,1]);
grouped, logs, it = cluster(x, 4)
plt.figure(figsize=(15,8))
for i in range(it):
plt.subplot(2, it//2+1, i+1) # row, col, index
df = pd.DataFrame(logs[i])
df.columns = ['x1', 'x2', 'group']
sns.scatterplot(data = df, x = 'x1', y = 'x2', hue = 'group').set_title(f'iter : {i}')
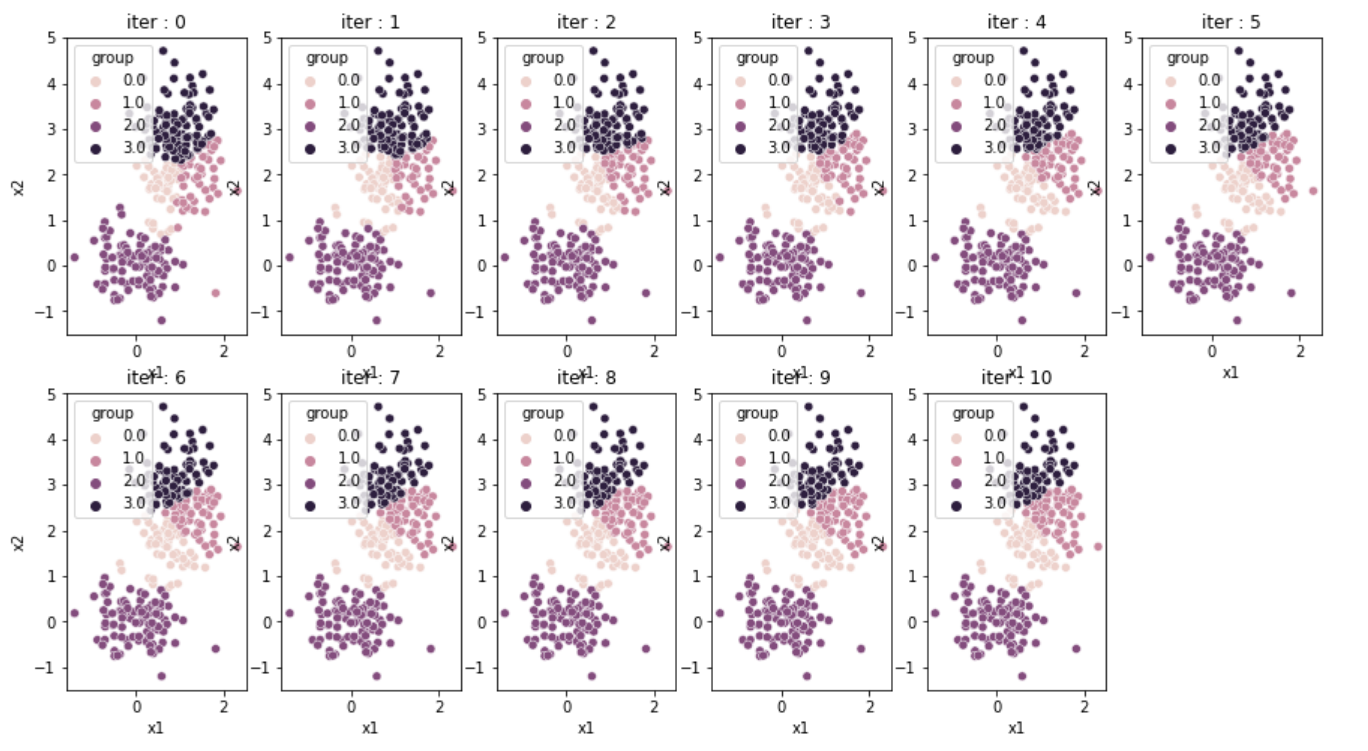 위와같이 k의 개수를 잘못 설정하면 다소 좋지않은 성능을 보여준다.
위와같이 k의 개수를 잘못 설정하면 다소 좋지않은 성능을 보여준다.
결과
- 확실히 rough하게 짠 알고리즘이다보니 성능(속도 측면)이 좋지않았다.
- 추가로 얼마나 잘 분류되었는지를 평가하는 척도를 통해 적절한 k값을 찾는 과정이 요구될 것이다.
