[Python] AdaGrad, RMSProp, Adam 구현

Abstract

딥러닝에서 각 노드의 weight를 조정할 때, batch마다 gradient를 계산해 일정 비율(learning rate)로 weight를 업데이트한다. 이때 learning rate값이 크면 weight는 발산하게되고, 또 너무 작으면 수렴하는속도가 느려 학습시간이 오래걸릴것이다. 그래서 gradient를 이용해 weight를 적절하게 업데이트 하는 여러가지 방법들이 있으며 여기서는 자주사용되는 AdaGrad, RMSProp, Adam 3가지 방법에 대해 소개하고자 한다.
또한 보다 직관적인 이해를 위해 실제 데이터를 이용한 딥러닝학습과정이 아닌 임의의 함수(f(x))를 설정하고, gradient(df(X)도 계산해 위와같은 방법을 통해 f(x)를 minimize하는 x값을 찾는 과정으로 진행한다.
상세 코드 참조 : https://github.com/parkeunsang/ML_algorithms/blob/master/ANN/optimizers.ipynb

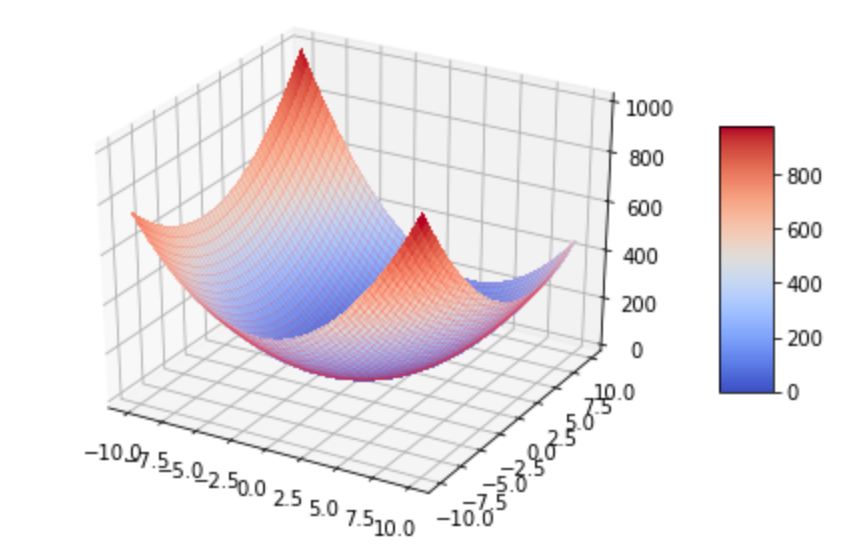
f(x)

먼저 f(x)를 아래와 같이 설정했다.

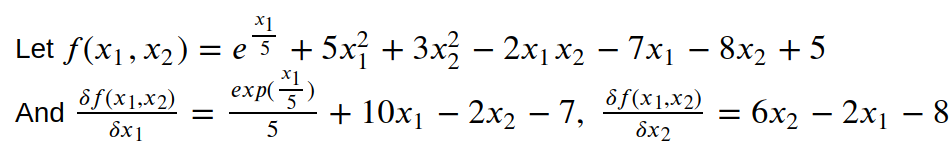sample images Code

#f(x1,x2)
def fx(x):
    x1 = x[0]
    x2 = x[1]
    return np.exp((x1)/5)+5*(x1**2) + 3*(x2**2) - 2*x1*x2 - 7*x1 - 8*x2+5
		
#gradient of f
def gfx(x):
    x1 = x[0]
    x2 = x[1]
    return np.array([np.exp(x1/5)/5+10*x1-2*x2-7, 6*x2-2*x1-8])

sample images

Plotting에 사용될 함수

def plotLog(log):  # weight가 업데이트되어가는 로그
    df = pd.DataFrame(log)
    df.columns = ['x','y']
    df['z'] = np.array(list(range(len(df))))
  #  df['z'] = np.log(df['z']+1)
    sns.scatterplot(
        data=df, x='x', y='y', hue='z'
    )

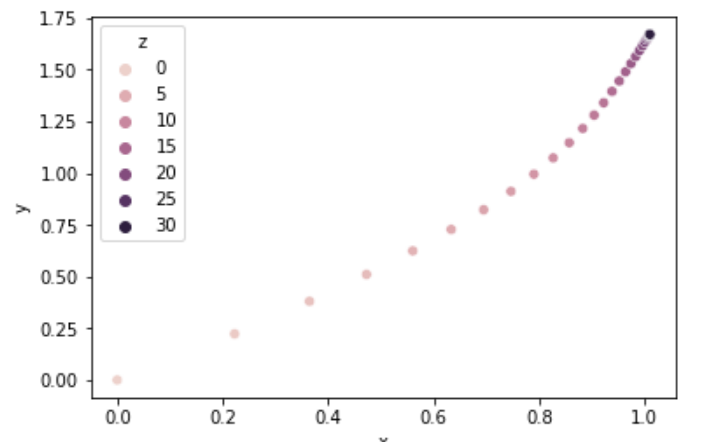
1. AdaGrad

weight를 업데이트할때 learning rate의 값을 계속 감소시켜나가는것(df^2와 관련) Code

def adagrad(f, gfx, x, ir=100, h=np.array([0.1,0.1]), lamb=0.1, th=0.00001):
    h = h.copy()
    log = np.array([])
    for i in range(ir):
        log = np.append(log, x)
        gx = gfx(x)
        h += gx**2
        xNew = x-lamb*gx/(h**(1/2))
        if(sum(abs(x-xNew)) <th):
            break
        x = xNew
    log = log.reshape(len(log)//2, 2)
    return x, i, log
x = np.array([0,0])  # init variable

xm, _, log = adagrad(fx, gfx, x, ir=1000)
plotLog(log)

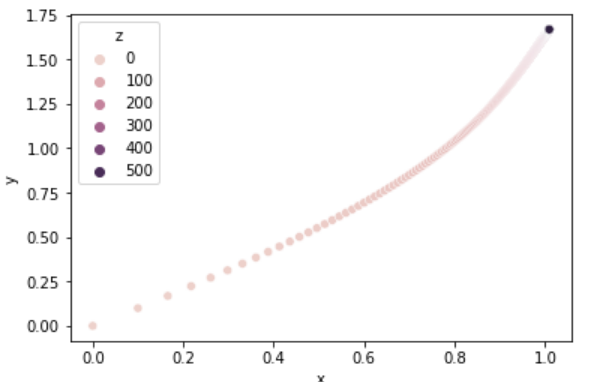
탐색 과정 sample images

시행횟수가 커질수록 업데이트속도가 느려진다. -> 오래걸림

2. RMSProp

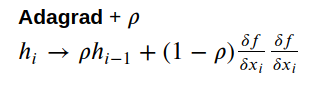
AdaGrad에서 h가 계속 커지는것을 방지하기위해 이전 h와 df^2의 비율을 정해 h를 업데이트 sample images

def rmsprop(f, gfx, x, ir=100, h=np.array([0.1, 0.1]), gamma=0.001, lamb=0.1, 
                    rho = 0.5, th=0.00001):
    h = h.copy()
    log = np.array([])
    for i in range(ir):
        log = np.append(log, x)
        gx = gfx(x)
        h = rho*h + (1 - rho)*gx**2
        xNew = x-lamb*gx/(h**(1/2))
        if(sum(abs(x-xNew)) <th):
            break
        x = xNew
    log = log.reshape(len(log)//2, 2)
    return x, i, log
x = np.array([0,0])
xm, _, log = rmsprop(fx, gfx, x, rho=0.8,ir=1000)
plotLog(log)

sample images

AdaGrad보다 수렴속도가 빠름

3. Adam

Momentum + RMSProp ref : ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION sample images

def adam(gfx, x, ir=1000, alpha = 0.1, beta1 = 0.9, beta2 = 0.999,
                epsilon = 10e-8, th=0.00001):
    m = 0
    v = 0
    t = 1
    log = np.array([])
    while t < ir:
        log = np.append(log, x)
        gx = gfx(x)
        m = beta1 * m + (1 - beta1) * gx
        v = beta2 * v + (1- beta2) * gx **2
        mh = m / (1 - beta1 ** t)  # m hat
        vh = v / (1 - beta2 ** t)  # v hat
        x_new = x - alpha * mh / (vh ** (1/2) + epsilon)
        if(sum(abs(x-x_new)) <th):
                break
        x = x_new
        t += 1
    log = log.reshape(len(log)//2, 2)
    return x, t, log
x = np.array([0,0])
xm, _, log = adam(gfx, x, alpha = 0.1)
plotLog(log)

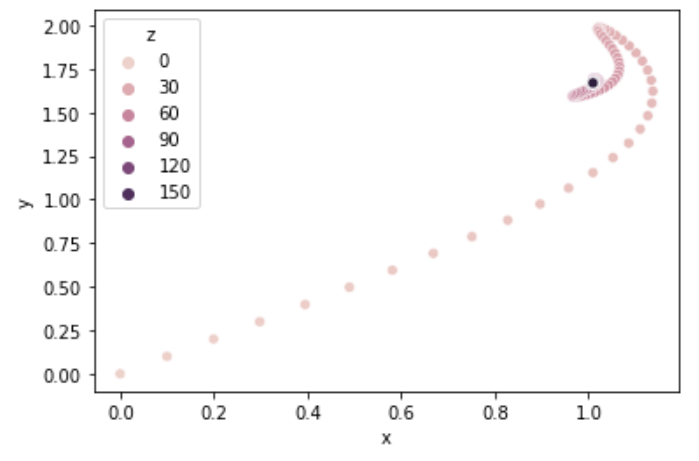
sample images

세 optimizer중 가장 최신 알고리즘

추가로 여러 local minimum이 있는 함수를 설정해 성능을 비교해볼 필요도 있음.