Intro

데이터분석을 하다보면 가설검정을 해야할 일이 많다. 여기서 가설검정이라 함은 사전에 귀무가설과 유의수준을 설정해 데이터 결과값을 토대로 귀무가설을 채택/기각하는 교과서에서 배운 딱딱한 가설검정뿐만 아니라 “내 주식 전략이 유효한 수익을 내는가?”와 같은 간단한 질문도 가설검정의 범위에 포함된다고 할 수 있다.
여기서는 후자의 예시를 통해 Bootstrap을 활용한 가설검정을 해보고자 한다.

Bootstrap이란

표본집단에서 n개의 샘플을 추출해 통계량을 계산하는 과정을 매우 많은 횟수로 반복(복원추출)한 결과의 분포는 정규분포를 따르고, 이를 가설검정에 활용할 수 있다.

삼성전자 주가 데이터를 활용한 예제

  • 원래는 일별 주가 등락률을 사용하려고 했으나, 이미 정규분포에 가까운 형태를 띄고 있어서 Bootstrap의 취지에 맞게 정규분포와 거리가 있는 거래량 데이터를 활용했다.
  • 가설은 "주가의 변동이 큰 다음날 거래량이 평소보다 많을까?"이다.

데이터 분포

import FinanceDataReader as fdr
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

df = fdr.DataReader('005930', '2015')  # 2015년 이후 삼성전자 주가 데이터
df['Volume'].plot(kind='hist', bins=100, xlim=(0, 5e+7))  # 거래량의 분포

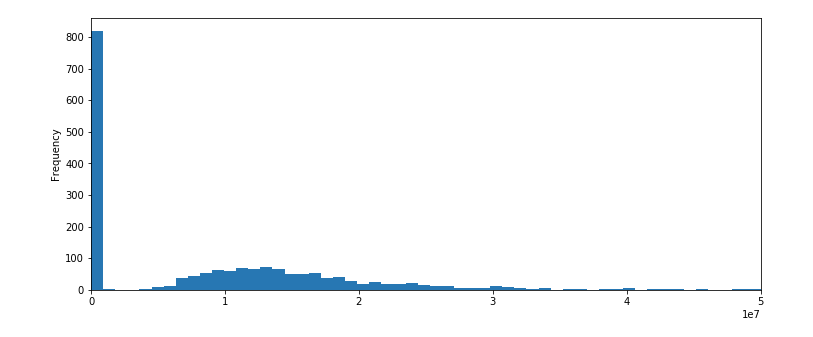
  • 데이터 기간:2015.01.01 ~ 2022.08.05
  • 일일 삼성전자 주식 거래량의 분포는 정규분포와는 거리가 있어 보인다.

주가 변동과 거래량

  • 주가 변동은 전날 고가와 저가의 변동폭(고가/저가 - 1)이 4%이상인 날을 기준으로 하였다.
df['variance'] = df['High'] /df['Low'] - 1
df['variance'] = df['variance'].shift(-1)
print(np.mean(df['variance'] > 0.04))  # 0.039572192513368985
print(df[df['variance'] > 0.04]['Volume'].mean())  # 17363760.283783782
df['Volume'].mean()  # 9148466.696791444
  • 변동폭이 4% 이상인 날의 빈도는 약 4%(0.0395…)이다.
  • 주가의 변동폭이 4%이상인 다음날 거래량의 평균은 약 1736만주 이다.
  • 위의 조건 없이 일반적인 삼성전자 주식의 거래량 평균은 약 915만주 이다.

주가 변동폭이 큰 다음날 거래량이 큰 것은 맞는것 같은데(약 2배차이) 이게 얼마나 유의미한 차이일까는 통계적으로 와닿지 않는다(얼마나 희박한 확률인가). 그래서 Bootstrap을 통해 이를 알아보고자 한다.

Bootstrap

n = int(len(df) *np.mean(df['variance'] > 0.04))  # 74
boot_list = []
for _ in range(10000):
    boot_list.append(df['Volume'].sample(n).mean())
boot_list = np.array(boot_list)
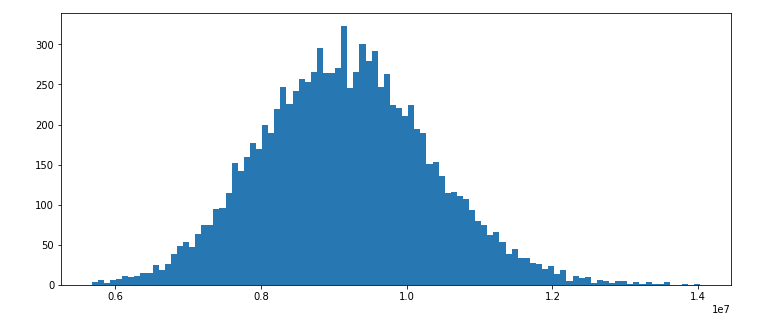
plt.figure(figsize=(12,5))
plt.hist(boot_list, bins=100);
  • 표본집단의 데이터 개수는 1870(len(df))이고, 전날 주가의 변동폭이 4%이상인 날은 74회였으므로 뽑는 샘플의 개수(n)은 74가 된다.
  • 총 10000번 반복한 결과의 분포는 아래와 같이 정규분포 형태를 보임을 알 수 있다.

가설검정

np.mean(boot_list > df[df['variance'] > 0.04]['Volume'].mean())  # 0.0
print(np.std(boot_list))  # 1178456.0974523935
print(np.mean(boot_list))  # 9161909.036206756
  • 먼저 rough하게 살펴보면, 10000번중에 샘플링된 74개의 거래량의 평균이 1736만이상 나온 경우는 0번임을 알 수 있다. 이를 통해 주가 변동폭이 4%이상인 다음날 거래량은 평소보다 높다고 제시할 근거가 충분하다고 볼 수 있다(만번중에 1번도 이렇게 크게 나오지 않음).
  • 표준편차가 약 118만이므로 단측검정일 때 거래량 평균값이 1152만 이상(평균 + 1.96*표준편차)이라면 유의수준 alpha가 0.025일때 귀무가설(주가의 변동폭이 4%이상인 다음날 거래량의 평균은 일반적인 거래량의 평균보다 높다.)을 기각할 수 있다.
  • 결과적으로 Bootstrap Method를 통해 1736만주라는 결과값이 얼마나 유의미한 지를 수치적으로 알 수 있다고 볼 수 있다.